Farmakologien der er læren om lægemidler kan deles op i to faggrupper kaldet Farmacodynamik og Farmacokinetik. Farmakodynamik er læren om hvad lægemidlet gør ved kroppen, mens Farmakokinetik er læren om hvad kroppen gør ved lægemidlet. I denne artikel beskrives hvad farmakodynamik handler om, dvs. den del der behandler hvad lægemidlet gør ved kroppen.

Klassisk okkupansmodel

I den klassiske okkupansmodel forestiller man sig et lægemiddel binder sig til en receptor og danner et lægemiddel-receptor-kompleks. Processen den ene vej og den anden vej antages at være reversibel og der forudsættes at være steady-state. Det forudsættes at der ikke sker interaktion mellem receptorerne.

D + R <-> DR

Hastighedskonstanten mod højre kaldes associationshastighedskonstanten k1 og hastighedskonstanten mod venstre kaldes dissociationshastighedskonstanten k2. Man definerer så en ny dissociationskonstant K_D som værende dissociationshastighedskonstanten k2 divideret med associationshastighedskonstanten k1.

K_D = k2/k1

I denne model gælder Langmuir ligningen:

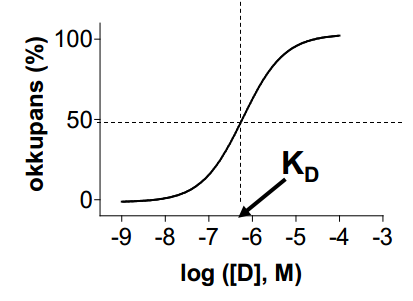
okkupansen = [DR]/[R_total] = [D]/([D] + K_D)

Hvor [DR] er konc. af lægemiddel-receptor-komplekset, [R_total] er konc. af totalt antal receptorer, [D] er konc. af lægemidlet og K_D er koncentrationen af lægemidlet hvor receptoren er 50% okkuperede. Man kalder også [DR]/[R_total] for okkupansen. Man definerer nu affiniteten eller potensen som:

affiniteten/potensen = -log(K_D)

Man kan nu afsætte okkupansen som funktion af affiniteten og få følgende graf (en dosis-okkupans-graf):

2-stadium modellen

I tostadiummodellen ser man receptoren som at kunne være i både et aktivt og et inaktivt stadie. Det betyder at hvis et lægemiddel binder til en inaktiv receptor og danner et lægemiddel-receptor-kompleks fører dette ikke til aktivering, hvorimod det gør det hvis receptoren er aktiv. Denne model er altså en rafinering af den klassiske okkupansmodel.

3-stadium modellen

I trestadiummodellen antager man yderligere at receptoren kan aktivere to forskellige typer G-proteiner enten G_alfa-s eller G_alfa-i.

Agonister og antagonister

En agonist er et lægemiddel der binder til en receptor og medierer en responsændring.

En antagonist er et lægemiddel der binder til en receptor og blokerer eller dæmper en agonist-medieret responsændring.

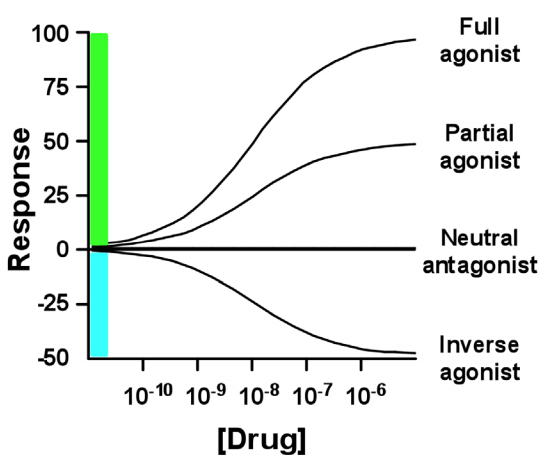
Man skelner mellem forskellige agonister:

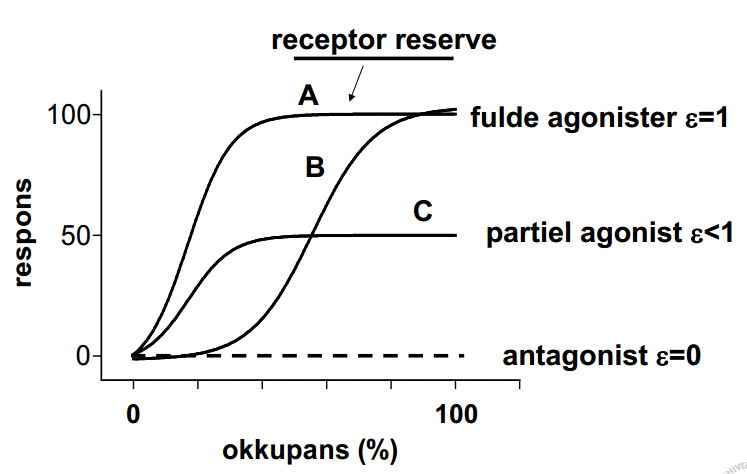
En fuld agonist er en agonist der kan give samme respons som den naturlige ligand. En partiel agonist giver kun delvist det respons en naturlig ligand gør. En neutral antagonist blokerer for den naturlige ligand. En invers agonist binder til receptoren, men giver en modsatrettet virkning.

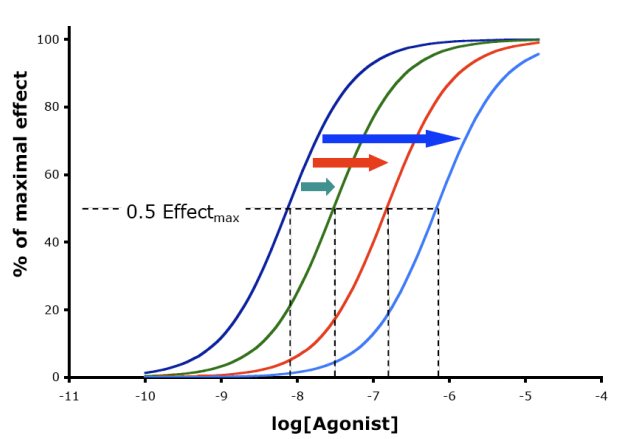
Hills ligning

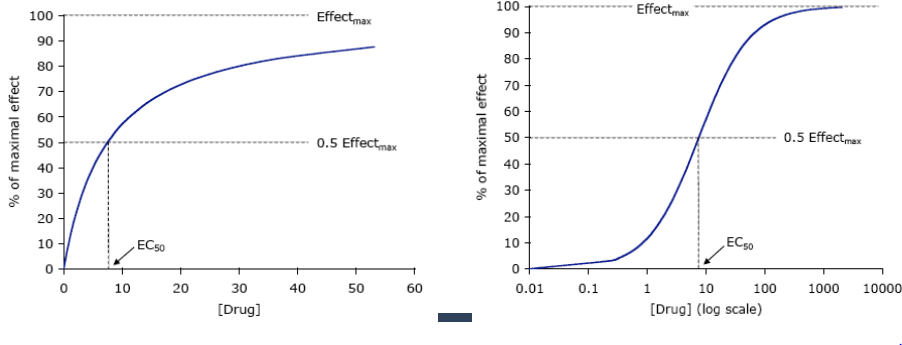
Hills ligning sammenholder det respons et lægemiddel giver med koncentrationen af lægemidlet i Hills ligning:

E/E_max = [A]^n / ([A]^n + EC50^n)

Hvor E er responset, [A] er konc. af lægemidlet, n er Hills konstant, E_max er maksimalt respons og EC50 er den koncentration der giver 50% af maksimalt respons.

Man kan nu afsætte respons som funktion af koncentrationen (evt. med logskala) og få en dosis-respons-graf.

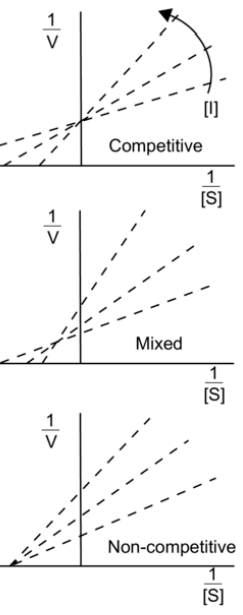
Antagonist typer

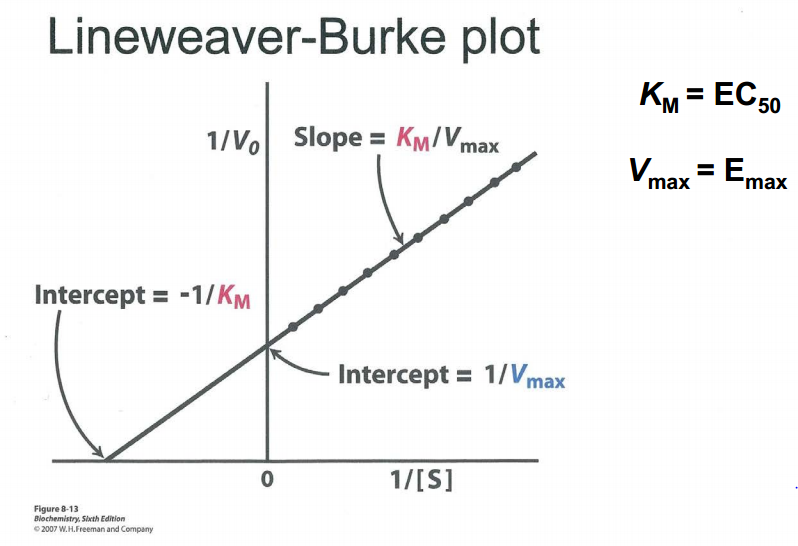
Man kan nu omskrive ligningen til noget der minder om Michaelis Menten kinetik for enzymer:

1/E = (EC50/E_max)*(1/[A]) + (1/E_max)

Nu kan man så lave et lineweaver-burke plot hvor man udfra en ret linje kan aflæse EC50 og E_max.

Nu kan man så sammenligne forskellige plots og finde ud af hvilken type antagonist et lægemiddel er:

En kompetetiv antagonist kæmper om pladsen i det aktive site med agonisten. Det betyder at antagonisten kan fortrænges af agonisten. En irreversibel non-kompetetiv antagonist konkurrerer ikke med agonisten og agonisten kan derfor ikke fortrænge antagonisten. En kompetetiv antagonist vil højreforskyde en dosis-respons graf.

Okkupans vs. respons

Der er ikke nogen egentlig direkte sammenhæng mellem okkupans og respons. Man kan altså ikke sige at 100% respons sker ved 100% okkupans, da der sagtens kan opnås 100% respons før 100% okkupans. Alligevel har Furchgott fremstillet en funktion, kaldet Transducer funktionen, som fortæller hvordan responset afhænger af okkupansen:

E = f((epsilon * [A] * [R_total])/([A] + K_D))

Hvor epsilon er en egenstimulerende virkning eller intrinsic efficacy, dvs. en konstant der er ligand og vævsafhængig.

Hvis der opnås 100% respons før der er 100% okkupans, kalder man det resterende antal frie receptorer for receptorreserven.

Hills ligning for antagonister

Man kan også opskrive Langmuir ligningen for et system hvor der både er en agonist og en kompetetiv antagonist til stede:

[AR]/[R_total] = [A]/([A] + K_A * (1 + [B]/K_B))

Hvor A er agonisten og B er den kompetetive antagonist. K_A er dissociationskonstanten for agonisten og K_B er dissociationskonstanten for antagonisten.

Man kan nu sammenligne langmuir ligningen for agonisten alene til stede og så ligningen for agonist og kompetetiv antagonist sammen. Her får man så følgende ligning:

[A]_1 / [A]_2 = 1 + [B]/K_B = CR

Hvor [A]_1 er koncentrationen af agonisten når antagonisten er til stede, [A]_2 er koncentrationen af agonisten når antagonisten ikke er til stede, [B] er koncentrationen af antagonisten og K_B er dissociationskonstanten for antagonisten. CR er dosisratioen eller koncentrationsratioen og er ratioen mellem agonistens konc. når antagonisten ikke er til stede og den er til stede. Man kan nu omskrive denne ligning til:

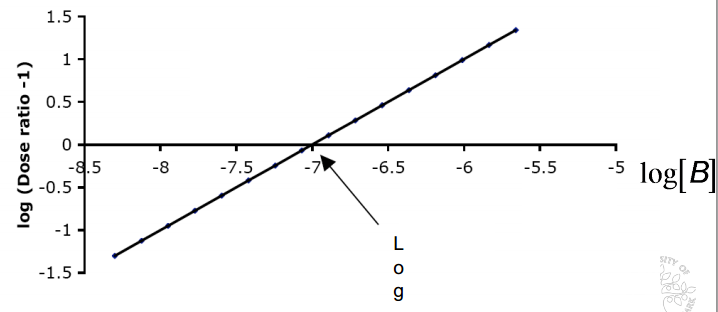
log(CR-1) = log[B] – log(K_B)

Hvilket kan give denne graf:

Hvor skæringen med x-aksen er log(K_B).

Man definerer nu -log(K_B) som Schilds konstant:

Schilds konstant = -log(K_B)

Schilds konstant er den negative logaritme til den konc. af antagonisten, som medfører at agonistens dosis skal fordobles, for at opnå samme effekt som når antagonisten ikke er til stede.

CR = 1 + [B]/K_B

Allosteriske modulatorer

En allosterisk modulator er en ligand som øger eller hæmmer virkningen af en primær agonist eller antagonist ved at binde til et allosterisk sted på receptoren. En allosterisk enhancer har ingen effekt selv, men øger affiniteten og/eller  maksimum effekt (efficacy) af den primære ligand. En allosterisk agonist er en ligand som kan foresage receptor aktivitet ved binding til et allosterisk binding site på receptoren.

Sidst opdateret 30. maj 2023