Henderson-Hasselbach ligningen kaldes også for pufferligningen og er nok den mest anvendte pH-formel i medicin. I denne artikel præsenteres ligningen kort og herudover bevises den.

Først vil jeg lige definere et generelt ligevægtssystem for en syre der reagerer med vand.

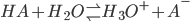
Her er HA en generel formel for en syre (H symboliserer at enhver syre kan afgive en proton) og A- er den deprotonerede, korresponderende base.

Dette er jo en kemisk ligevægt og derfor kan vi opskrive ligevægtsloven for denne:

Bemærk her at vand ikke deltager i ligevægtsloven, da det er solvent og derfor indgår i ligevægtsloven med 1. K_a er syrestyrkekonstanten. Vi ved at vi også kan tage -log til denne og så kalder vi den for pKa.

Hvis man tager logaritmen til et produkt, er det det samme som summen af logaritmen af hver faktor (dvs. 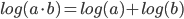).  Vi får:

-log[H3O+] er jo pH:

Vi kan nu isolere pH:

Hvornår gælder Henderson-Hasselbach ligningen?

Vi kan se at Henderson-Hasselbach ligningen egentlig bare er ligevægtsloven i forklædning. Det betyder at den kræver blot at der er ligevægt (da det er her ligevægtsloven gælder) og at reaktionen ikke forløber fuldstændigt (da [HA]=0 og der derfor står 0 i nævner) eller slet ikke (da [A-] = 0 og log(0) er ikke defineret). Den beregner pH i en opløsning hvor både en syre og dens korresponderende base er til stede. En sådan opløsening kalder vi for en pufferopløsening og dem er der flere af i kroppen, hvoraf bikarbonatsystemet er det største.

Ioniseringsgraden

Bemærk også at Henderson-Hasselbach ligningen siger noget om ioniseringsgraden af lægemidler, dvs. hvor meget der findes på deprotoneret eller protoneret form ved en bestemt pH. Dette er følgende forhold:

Nogle gange definerer man ogsåå ioniseringsgraden som den deprotonerede andel i forhold til den totale mængde syre. Det angives ofte i procent:

(Ioniseringsgrad=frac{[A^-]}{[A^-]+[HA]})

På den måde kan man regne ud om et lægemiddel forholdsvis vil være på henholdsvis protoneret eller deprotoneret form i f.eks. maven (pH=2) eller tyndtarmen (pH=5).

Sidst opdateret 30. maj 2023