Nogle generelle regneregler – helt tilbage fra folkeskolen og gymnasiet – anvendes næsten hele tiden i forbindelse med udledning af formler. Tilbage i gymnasiet udgav jeg en formelsamling med helt generelle regneregler. Disse samler jeg nu på denne side. Dette er altså de helt basale regneregler alle bør kunne.
Basale regneregler
Logaritmeregneregler
- Logaritmen til 1 er altid lig med 0 – uanset hvilket grundtal x man anvender ved logaritme.
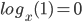
- Logaritmen til grundtallet er lig med 1.
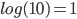
- Logaritmen til et produkt er lig med summen af logaritmerne til hver faktor.
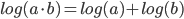
- Logaritmen til en brøk er lig med differencen mellem logaritmen til tæller og logaritmen til nævner.
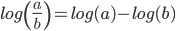
- Logaritmen til en potens er lig med eksponenten gange logaritmen til grundtallet.
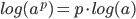
- Man kan skifte grundtal ved at dividere med logaritmen til det nye logaritme-grundtal.
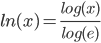
Brøkregneregler
- Vil man lægge to brøker sammen skal man først finde en fællesnævner og så lægge tællerne sammen.
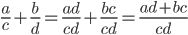
- Man ganger et tal med en brøk ved at gange den ind i tæller.
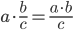
- To brøker divideres med hinanden ved at putte tællers nævner ned i nævner og nævners nævner op i tæller.
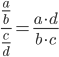
- Man ganger to brøker sammen ved at gange tæller med tæller og nævner med nævner.
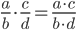
- Står der 0 i tæller giver hele brøken 0.
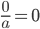
- Man kan ikke dividere med 0.
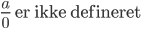
Potensregneregler
- Man ganger to potenser med samme grundtal sammen ved at lægge eksponenterne sammen.
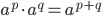
- Man dividerer to potenser med samme grundtal ved at trække eksponenterne fra hinanden.
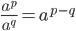
- Man opløfter en potens til en ny eksponent ved at gange eksponenterne sammen.
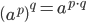
- En potens med eksponent 0 giver altid 1.
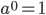
- Et produkt opløftet i en eksponent er lig med hver faktor opløftet i eksponenten og ganget sammen.
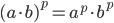
- En negativ eksponent er det samme som den reciprokke værdi af potensen med den positive eksponent.
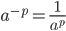
Kvadratrodsregneregler
- En kvadratrod er det samme som en potens med eksponent ½.
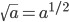
- Kvadratroden af et produkt er det samme som produktet af kvadratroden af hver faktor.
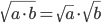
- Kvadratroden af en brøk er det samme som en brøk med kvadratrod af henholdsvis tæller og nævner.
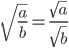
- Man kan ikke tage kvadratroden til et negativt tal (i hvert fald ikke hvis resultatet skal være et reelt tal).
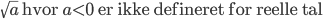
Ophævelse af parenteser
- Kvadratet på en 2-ledet størrelse – man tager det første led i anden plus det andet led i andet plus eller minus det dobbelte produkt.
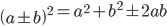
- Man ganger ind i en parentes ved at gange ind i hvert led.
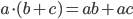
- Står der minus foran en parentes ophæves parentesen ved at skifte fortegn på alle led i parentesen.
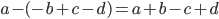
- Står der plus foran en parentes kan den blot ophæves.
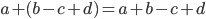
- To parenteser ganget med hinanden løses ved at gange ledvist mellem hver parentes.
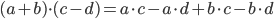
Geometri og trigonometri
Retvinklede trekanter
- Pythagoras læresætning gælder for retvinklede trekanter, hvor a og b er kateter og c er hypotenuse.
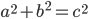
- Sinus til en vinkel er lig med modstående katete divideret med hypotenusen.
sin(v) = mod/hyp
- Cosinus til en vinkel er lig med hosliggende katete divideret med hypotenusen.
cos(v) = hos/hyp - Tangens til en vinkel er lig med modstående katete divideret med hosliggende katete – eller sinus divideret med cosinus.
tan(v) = mod/hos = sin(v)/cos(v)
Generelle trekanter
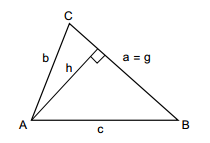
- Sinusrelationerne siger at forholdet mellem en side og sinus til modstående vinkel altid vil være den samme.
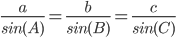
- Cosinusrelationerne eller pythagoras udvidede læresætning:
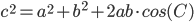
- Arealet af en trekant er en halv højde gange grundlinjen.
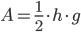
- Arealet af en trekant er en halv gange produktet af 2 sider og sinus til modstående vinkel til den sidste side:
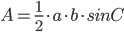
Rektangler
- Arealet af et rektangel er længde gange bredde.
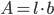
- Omkredsen af et rektangel er lig med 2 gange summen af længde og bredde.
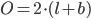
Trapez
- Arealet af en trapez er lig med en halv gange højde gange summen af de to parallelle sider.
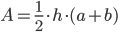
Parallelogram
- Arealet af et parallelogram er lig med højden gange grundlinjen.
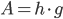
Cirkel
- Arealet af en cirkel er lig med pi gange radius i anden.

- Omkredsen af en cirkel er lig med 2 gange pi gange radius.
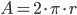
Cylinder
- Volumen af en cylinder er lig med pi gange radius i anden gange højden.
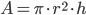
- Den krumme overflade O er lig med 2 gange pi gange radius gange højden.
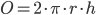
Kegler
- Volumen af kegler er lig med 1/3 af højden gange grundfladearealet G.
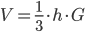
Pyramide
- Volumen af en pyramide er lig med 1/3 af højden gange grundfladearealet G.
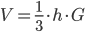
Kugle
- Volumen af en kugle er 4/3 gange pi gange radius i tredje.
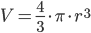
- Overfladearealet O af en kugle er lig med 4 gange pi gange radius i anden.
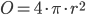
Funktioner
Lineær funktion
- Ligning for en lineær funktion:
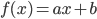
- Løsning til en lineær ligning:
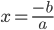
- Hældning:
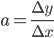
- Konstantled:
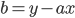
Hyperbel
- Ligning for hyperbel:
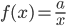
Andengradspolynomium
- Ligning for andensgradspolynomium:
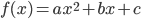
- Løsning for andengradsligning hvor diskriminanten
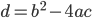 :
: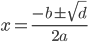
- Toppunkt:
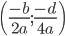
Vektorregning
Generelle vektorformler
- Længden af en vektor finder man ved kvadratroden af kvadratet på hver koordinat:
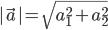
- Man ganger et tal med en vektor ved at gange tallet ind i hver koordinat:
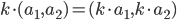
- Summen af to vektorer findes ved at summere hver koordinat:
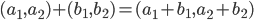
- Differencen mellem to vektorer findes ved at tage differencen af hver koordinat:
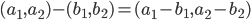
- Skalarproduktet/prikproduktet sker ved at gange samme koordinater og så lægge produkterne sammen.
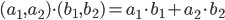
- Vinklen mellem to vektorer er prikproduktet divideret med produktet af længerne:
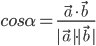
- Hvis to vektorer er vinkelrette (ortogonale) er prikproduktet 0.
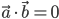
- Projectionen af vektor b på a:
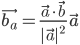
- Længden af en projektion:
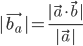
- Tværvektoren/Hatvektoren:
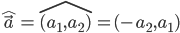
- Determinanten:
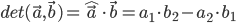
- Determinanten:
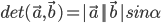
- Determinanten er lig med 0 ved parallelle vektorer:
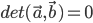
- Arealet af det parallelogram der udspændes af to vektorer:
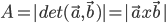
- Krydsproduktet:
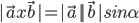
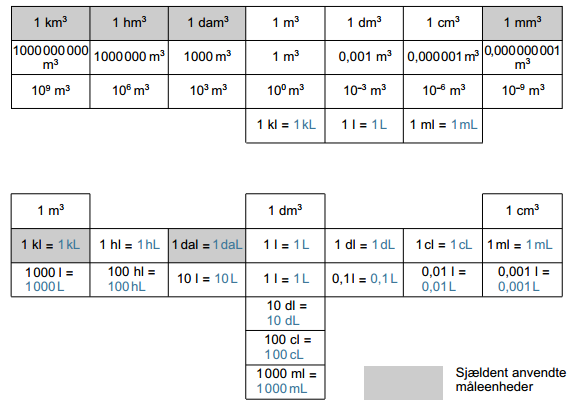
Data og enheder
Volumen
Sidst opdateret 30. maj 2023
